

At frequencies near the cutoff frequency, the impedance of the capacitors is comparable to the resistance of the resistors, and the positive-feedback path provided by C2 allows the circuit to generate the higher-Q type of response that we expect from resonance-based filters.

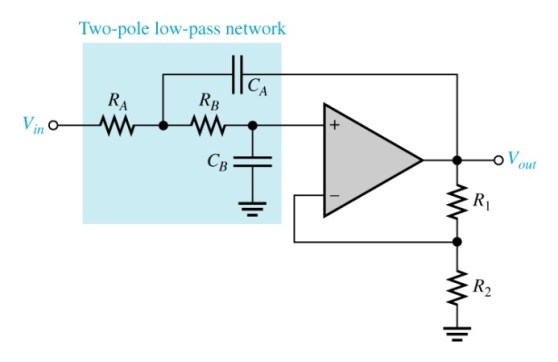
In both cases, the op-amp produces a buffered version of the output of the RCRC filter. High frequencies are shorted to ground, and low frequencies are passed to the input of the op-amp.If we ignore the positive-feedback path, the circuit is a second-order RC low-pass filter connected to a voltage follower.The qualitative operation of the unity-gain Sallen-Key low-pass filter becomes clear if you combine the preceding discussion with the fact that the negative-feedback path is a direct connection from the output node to the inverting input terminal: A Q factor of 0.5 is often unacceptably low, and the Sallen-Key architecture overcomes this limitation by using positive feedback to enable higher Q. This positive feedback allows the filter to overcome the fundamental limitation of the RCRC second-order low-pass filter: even when a buffer is placed between the two RC stages, the filter’s Q factor cannot exceed 0.5. The only difference is that C2, instead of creating a high-frequency path to ground, creates a high-frequency path for positive feedback. Notice that the passive components resemble a typical second-order RC low-pass filter. Nevertheless, we can acquire a general understanding of the circuit’s operation by performing non-mathematical analysis. We’re accustomed to analyzing op-amp circuits that have only negative feedback.Ī detailed analysis of the Sallen-Key low-pass filter is not particularly straightforward. There are two feedback paths, one of which is directed toward the op-amp’s non-inverting input terminal. We call these filters “active” because they include an amplifying component. As you can see, it requires only one op-amp, two resistors, and two capacitors. The following schematic is a unity-gain Sallen-Key low-pass filter. We could use this circuit to replace the inductor in a second-order RLC (resistor-inductor-capacitor) filter, but instead, we’ll look at a simpler and more compact topology known as the Sallen-Key filter. This circuit is an op-amp–RC resonator: it produces resonance using only resistance, capacitance, and amplification. The following diagram shows an op-amp-based circuit that functions as an inductor (the inductance is determined by the values of the passive components).

It turns out that the effect of inductance can be duplicated by combining an op-amp with clever circuit design. However, engineers often try to avoid the use of inductors relative to resistors and capacitors, they are larger, more susceptible to EMI, more likely to generate problematic EMI, and less compatible with integrated-circuit techniques. Higher-order filters can be achieved by taking advantage of the resonance that results from the interaction of capacitance and inductance. When system requirements cannot be met by a first-order filter, the designer must consider a second-order (or third-order, or fourth-order.) filter. These passive filters are easy to design and analyze, and they offer performance that is adequate in many applications. First-order low-pass and high-pass filters require nothing more than resistors and capacitors.


 0 kommentar(er)
0 kommentar(er)
